Abstract
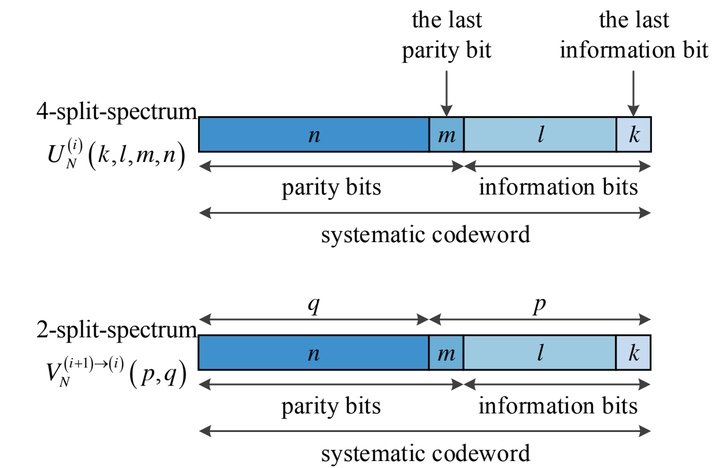
Code construction is a critical issue for polar coding. The expected construction method is of an accurate estimate of the reliability of bit-channels, but the current methods usually require high computational complexity. In this paper, we concern the input-output weight distribution of each bit-channel and derive its recursive calculation algorithm for systematic coding. The union bound and union-Bhattacharyya bound on the bit error probability are also derived to evaluate the reliability of bit-channels. Furthermore, by calculating the logarithmic form of the union-Bhattacharyya bound, we also propose two novel construction methods named the union-Bhattacharyya bound weight of the bit error probability (UBWB) and the simplified UBWB (SUBWB). Numerical results show that the proposed UBWB/SUBWB construction methods can achieve comparable performance to current methods under successive cancellation (SC) decoding and obtain obvious performance gain under SC list (SCL) decoding.